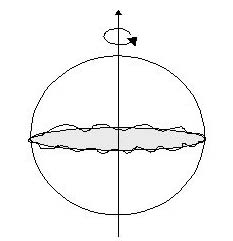２次元球面をN次元の正方行列で表示したものをファジィ球面とよびます．Nが十分に大きいと，これはスムースな球面とみなせますが，Nが有限のときは，非可換な座標をもつ球面となります．高エネルギー極限では，空間が非可換であると考えられているので，このようなファジィ球面は高エネルギー物理学の研究対象となっています．とくに，ファジィ球面上で何か物理量を計算できれば，その値から，高エネルギー極限での物理量が予測できるのではないかと期待されています．実際には，時空間は４次元なので，２次元のファジィ球面はいわゆる「おもちゃ」の模型を与えるにすぎませんが，非可換な空間における物理量を行列で計算できるという点は非常に魅力的かつ実践的です．

ここでは，「おもちゃ」の模型の１つとして，あるトポロジカルなゲージ理論をもちいて，ファジィ球面の赤道におけるゲージ場の揺らぎを計算しました（左図参照）．解析には行列計算のプログラミングに適したRと呼ばれるフリーのソフトをもちいました．Rスクリプトはここにあります．行列の次元Nは，解析時における積分変数の数と対応します．計算能力上，Nの値は20未満に制限されるため，ここではNを7, 9, 11, 13に指定しました．また，積分範囲を±0.5とし，赤道を360分割した時の30ステップ分のデータのみを計算しました．計算機の能力が向上すれば，行列の次元や積分範囲をさらに大きな値に取ることができるはずです．これらのインプット・データはスクリプトの冒頭で決めることができます．