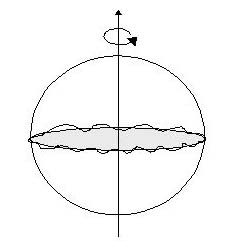A fuzzy S² is a matrix realization of the two-dimensional spherical surface S². If the matrix dimension N is large enough, the fuzzy S² becomes an ordinary smooth S². But if N is finite, this fuzzy space realizes a noncommutative S². In an extremely high-energy world, spacetimes are considered to be noncommutative. So the fuzzy S² provides an interesting research topic in high energy physics. Particularly, given that we can calculate some physical quantities on the fuzzy S², then it is expected that we may predict some physical values in an extremely high-energy world. In reality, spacetimes are in four dimensions and the fuzzy S² merely provides "toy" models. But the fact that physical quantities on a noncommutative space can be calculated in terms of matrices by itself is of great interest and of practical use.

Here, as one of such "toy" models, we compute fluctuations of gauge fields from the equator of the fuzzy S² in a certain topological gauge model. (See the left figure for a image of computation.) The analysis is carried out with a free softwear called R, which contains useful packages for matrix calculations. A script is given here. The matrix dimension N corresponds to the number of integral variables in the analysis. Owing to limited computational capability, this number should be below 20. In the present calculation, we choose N = 7, 9, 11, 13. We also fix the range of integrals between ±0.5 and show just 30-step data of the total 360 steps along the equator. The size of matrices and the range of integrals could be made larger with future developments in computational ability. These input data can be determined in the beginning of the script.